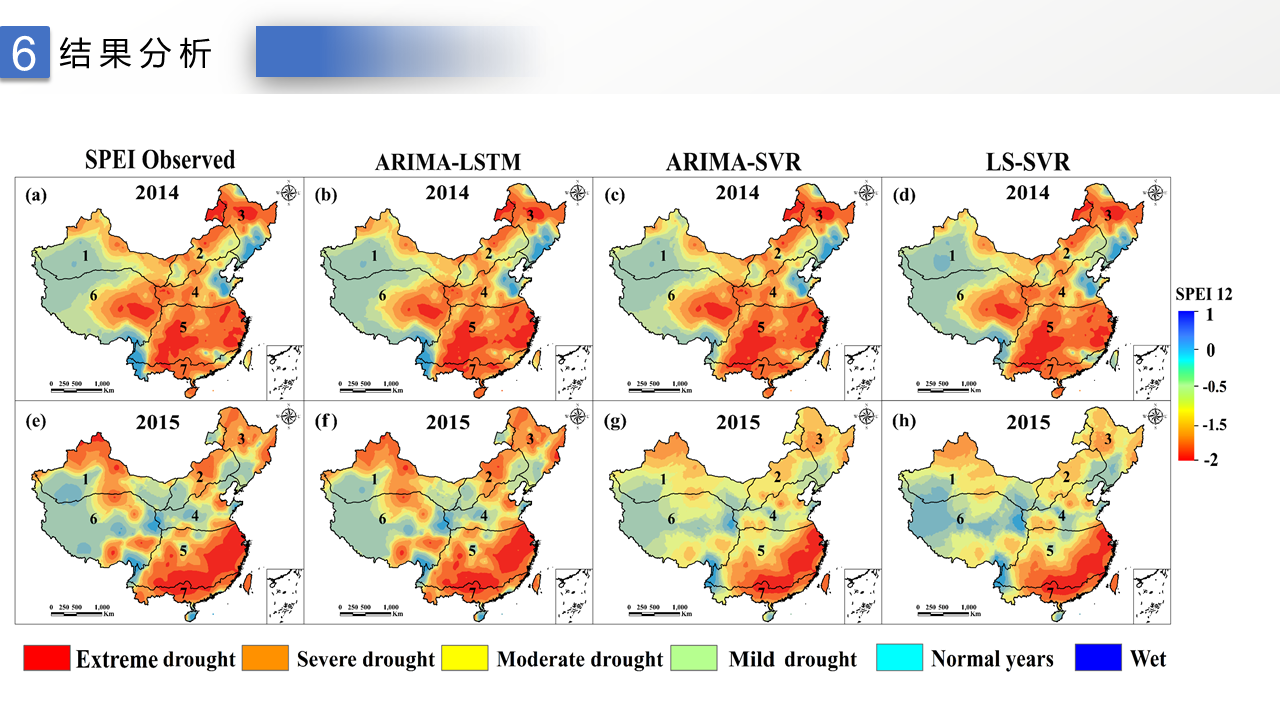
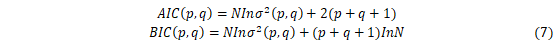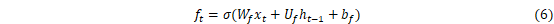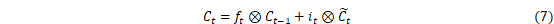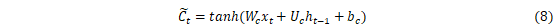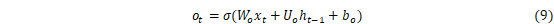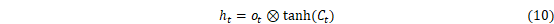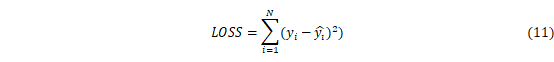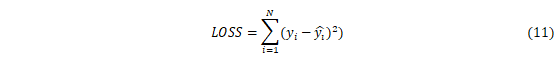由于中国各地旱情均有季节区分并且在旱情严重地区均有连旱情况发生,而大部分农作物生长季在3月到8月,因此本文分别计算了1980-2019年的1, 3, 6, 9, 12和24个月的SPEI值以及PDSI、PMDI、PHDI、Z-index、sc-PDSI的值,并通过国家标准气象干旱等级(GB/T20481-2006)规定的干旱分级标准(表1)来表征干旱情况[3]。表1 标准化降水指数干旱分级
Tab.1 Drought classification based on SPI
等级 | 类型 | 指数范围 |
1 | 无旱 | 指数≥-0.5 |
2 | 轻旱 | -1.0≤指数<-0.5 |
3 | 中旱 | -1.5≤指数<-1.0 |
4 | 重旱 | -2.0≤指数<-1.5 |
5 | 特旱 | 指数≤-2.0 |
3.2 时空模式挖掘
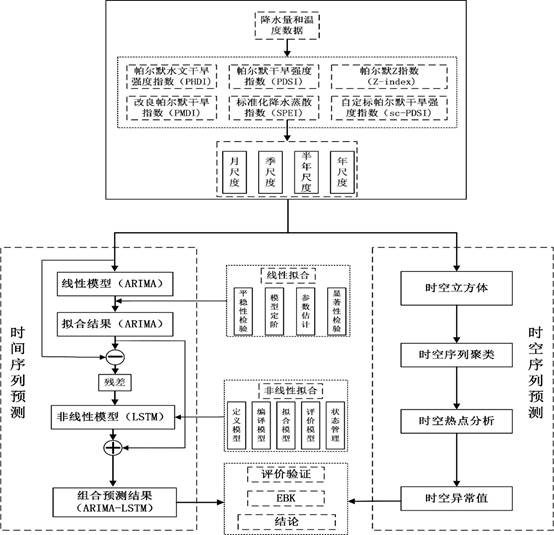
结合时空分析思维模式来探究气象干旱在中国的时空分布特征、时空演化过程、时空聚类分析和时空热点分析,能够为有关部门防旱抗旱提供科学依据。以下研究方法均从时空尺度出发并结合SPI对中国近40年气象干旱时空特征进行研究与分析。3.2.1 时空立方体
时空立方体模型是通过将样本点聚合到时空条柱的方法,形成NetCDF(Network Common Data Form),即网络通用数据格式的时空数据结构中[18]。通过创建时空立方体,能以时间序列分析、集成空间和时间模式分析等形式,对时空数据进行可视化与分析[18](见图2)。图2中x和y轴代表该时间段的空间位置,z轴代表时间,且最下面的为起始时间,最上面的为最近时间,每个立方体均由该时间对应的属性值组成,数值的大小可以通过设置不同颜色来区分。本文通过将气象站点数据计算得到的SPI值进行聚合,每年的SPI值均聚合到一个立方体中,而多个立方体按照时序排列(垂直排列)并聚合后得到时空柱,即每个站点形成一个时空柱。因此通过聚合不同时间尺度的SPI值,可得到中国612个气象站点监测到的不同类型的旱情。
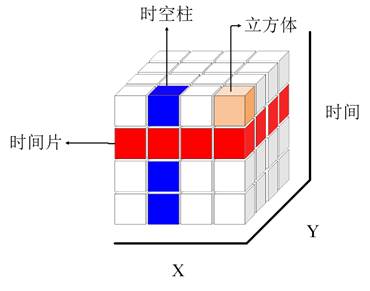
图2 时空立方体模型
3.2.2 时空序列聚类
在时空立方体的基础上,基于时间序列的相似特征,将时空立方体中的时间序列集合进行划分,也就是K-means算法的时空体现,其中每个聚类的成员具有的时间序列特征均相似。可以基于三个条件聚集时间序列:具有相似的时间值,趋于同时增加和减少以及具有相似特征的重复模式[19]。本文对1980-2019年SPI3、SPI6和SPI12结合时空立方体模型进行时空聚类,首先对中国612个气象站点创建泰森多边形,同时结合K近邻算法和K-means算法对612个泰森多边形进行聚类,聚类数目利用伪F统计量来选取,伪F统计量是一个反应聚类间方差和距离内方差的比率,即反应组内相似性和组间差异的比率。其值越大,表示该聚类数越有效。公式如下: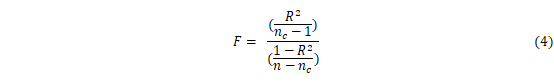
其中:

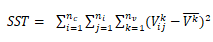
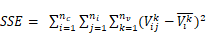
n=要素数,ni=聚类i中的要素数,nc=类(聚类)数,nv=用于聚类要素的变量数, =i聚类中j要素的k变量值,
=i聚类中j要素的k变量值,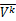 =k变量的平均值,
=k变量的平均值, =聚类i中k变量的平均值。
=聚类i中k变量的平均值。
3.2.3 时空热点分析
时空热点分析可识别数据的时空趋势,探测某一特征在时空尺度的热点或冷点,在本文中,热点代表该地区往年未有旱情或旱情不明显,而近年发生旱情或相比往年旱情严重的情况,而冷点则相反。通过特定的邻域距离和临域时间步长参数来计算每个立方体条柱的Getis-Ord Gi*统计量[20-21]。结合M-K检验法对时空尺度的热点分析结果进行趋势检验,共有17种,分别为新增的、连续的、加强的、持续的、逐渐减少的、分散的、振荡的以及历史的热点和冷点[21],还有一个是无显著特征。由于研究方向不同,因此本文共检验出6种,分别为:新兴热点、分散热点、振荡热点、新兴冷点、振荡冷点和无显著特征。
3.2.4 经验贝叶斯克里金插值法(EBK)
EBK是一种地统计插值方法,专为克服经典克里金法更加困难的理论和实践局限而开发的,它可以用构造子集和模拟的方法自动计算这些参数,而不需要像其它克里金插值法那样手动调整参数,并且可以通过估计基础半变异函数来说明引入的误差,因此EBK法与其他克里金相比预测精度更高[22]。3.3 时间序列预测
3.3.1 ARIMA模型
ARIMA分为自回归模型(Autoregressive model,AR)、滑动平均模型(Moving average model, MA)以及自回归移动平均模型(Autoregressive Moving Average Model, ARMA),是传统的时间序列预测模型。其建模流程是首先判断模型平稳程度,其次利用差分法对非平稳时间序列进行平稳化处理,然后选取AR(p),MA(q)对模型进行定阶,差分次数记为d,ARIMA(p,d,q)模型就是经过了d阶差分后的ARMA(p,q)模型。如下式所示: 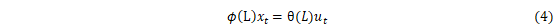
(4)中θ(L)和ϕ(L)分别为:


ARIMA(p,d,q)模型的一般式:
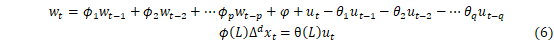
上式中,d为差分次数, 为自回归系数,p为自回归阶数,
为自回归系数,p为自回归阶数,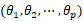 为移动平均系数;ut为白噪声序列(服从0均值、正态分布且相互独立的白噪声序列)。
为移动平均系数;ut为白噪声序列(服从0均值、正态分布且相互独立的白噪声序列)。
其中,p,q阶数采用赤池信息准则(Akaike Information Criterion, AIC)和贝叶斯信息准则(Bayesian Information Criterion, BIC)来确定,当样本数N固定时,选择AIC和BIC最小值来确定p,q。公式如下:
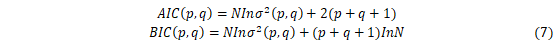
3.3.2 LSTM模型
LSTM是RNN的一种拓展,结构见图2。LSTM与RNN最大的不同在于隐藏模块中添加了三个门层,分别是忘记门(Forget gate)、输入门(Input gate)和输出门(Output gate)。忘记门决定什么样的信息保留,什么样的信息遗忘;输入门用来更新细胞状态,决定什么值我们需要更新;输出门是一个过滤器,基于我们的细胞状态来选择哪个部分用来输出。其中LSTM隐藏层结构如图3所示,其计算方法可以表示为[27]:
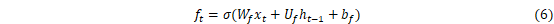
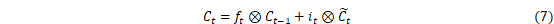
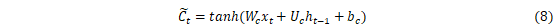
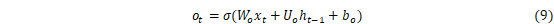
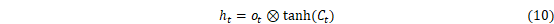
式中:i、f、C、o分别表示为输入门、遗忘门、细胞状态、输出门;W和b分别为对应的权重系数矩阵和偏置项;σ和tanh分别为sigmoid和双曲正切激活函数。
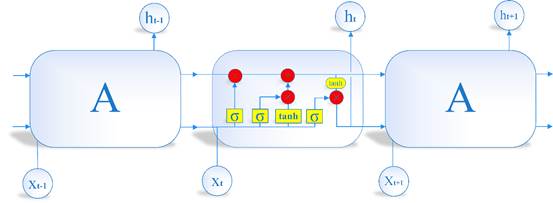
图 3 LSTM模型结构图
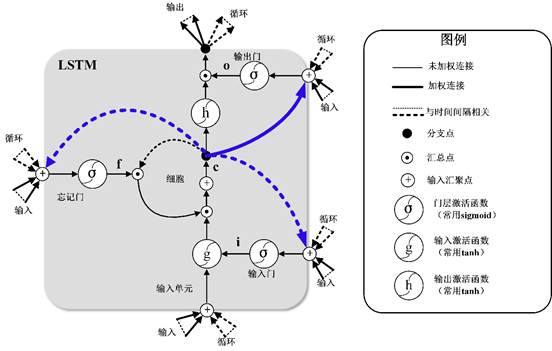
图 4 LSTM隐藏层细胞结构
本文利用LSTM对多时间尺度SPI序列进行拟合,由于LSTM的隐含层数量决定了模型拟合能力,为了防止过拟合,本文提出了“早停法”,即当损失函数不再下降时停止训练。损失函数定义如下: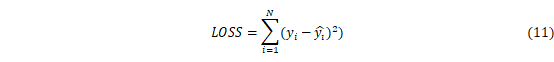
式中:在时间i处的观测值,是在时间i处的预测值。
建模流程如下:
·输入数据的预处理
通常,神经网络模型处理的数据是归一化数据,范围在[-1,1]。因为归一化可以使学习率不必再根据数据范围做调整,从而提高模型的训练速度。·参数率定与训练
本文基于Python3.7平台来搭建LSTM网络,采用基于时间的反向传播算法进行训练。batch_size设置为1,其中1代表在每个样本之后更新权重,该过程称为随机梯度下降(Stochastic Gradient Descent, SGD)。激活函数通常有sigmoid、tanh和relu,由于sigmoid在反向传播时很容易出现梯度消失情况,而tanh的SGD收敛速度太慢,因此本文选用relu做激活函数。由于本文选用“早停法”来防止训练过拟合,该方法选取均方误差(Mean Squared Error, MSE)作为损失函数,损失函数越小,说明预测模型精度越高,随着迭代次数不断增加时MSE值逐渐下降,直到某一时刻MSE值上升时说明模型过拟合,因此早停法在模型MSE值上升前一刻停止训练以保证预测模型的精度达到最高。迭代次数本文设置为300次,以保证MSE能降到最低。对于LSTM网络而言,神经元隐藏层数量决定着网络训练速度与预测精度,隐藏层数量太少,导致网络无法训练或效果很差,隐藏层数量过大又导致网络训练速度慢或者出现过拟合现象。本文采用黄金分割法来选择隐藏层神经元数量。黄金分割法是指在区间[a,b]中找到理想的隐含层节点个数,然后根据黄金分割原理扩展搜索区间,即得到区间[b,c](b=0.619*(c-a)+a)。·网络输出与评价验证
由于数据在预处理时采用归一化处理,因此对LSTM模型残差预测完毕后,得到的并不是最终结果,还需将该时间序列数据进行反归一化处理,即得到模型实际输出。经过交叉验证得到80%(1951.1—2004.8)数据作为训练集,20%(2004.9—2017.12)数据作为测试集。
3.3.3 ARIMA-LSTM模型
由于ARIMA模型和LSTM模型在线性和非线性预测中各有优点,因此本文分别采用ARIMA与LSTM模型的优点建立组合模型ARIMA-LSTM,假设时间序列可视为线性自相关部分与非线性残差两部分的组合,利用ARIMA模型对SPI值进行预测,将结果与实际值相减得到残差,将残差记为非线性部分,将残差带入LSTM模型进行预测,最后把两者预测结果相加得到组合结果,即:

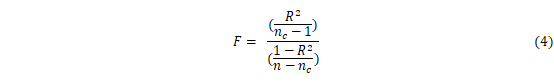

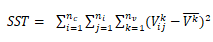
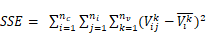
 =i聚类中j要素的k变量值,
=i聚类中j要素的k变量值,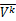 =k变量的平均值,
=k变量的平均值, =聚类i中k变量的平均值。
=聚类i中k变量的平均值。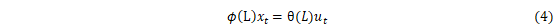


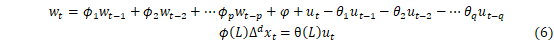
 为自回归系数,p为自回归阶数,
为自回归系数,p为自回归阶数,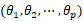 为移动平均系数;ut为白噪声序列(服从0均值、正态分布且相互独立的白噪声序列)。
为移动平均系数;ut为白噪声序列(服从0均值、正态分布且相互独立的白噪声序列)。